本篇文章是益智的教程,参考之后动手进行实践了一遍。编译环境windows10+python3.5
数据预处理
|
|
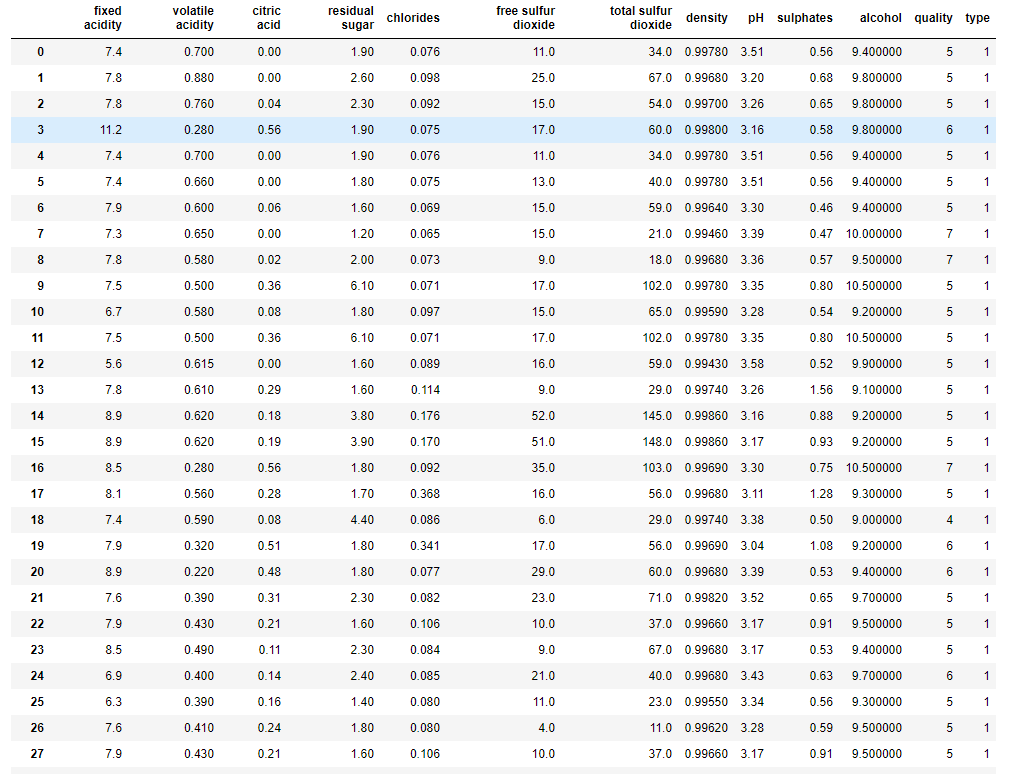
<bound method DataFrame.info of fixed acidity volatile acidity citric acid residual sugar chlorides \
0 7.4 0.700 0.00 1.9 0.076
1 7.8 0.880 0.00 2.6 0.098
2 7.8 0.760 0.04 2.3 0.092
3 11.2 0.280 0.56 1.9 0.075
4 7.4 0.700 0.00 1.9 0.076
5 7.4 0.660 0.00 1.8 0.075
6 7.9 0.600 0.06 1.6 0.069
7 7.3 0.650 0.00 1.2 0.065
8 7.8 0.580 0.02 2.0 0.073
9 7.5 0.500 0.36 6.1 0.071
10 6.7 0.580 0.08 1.8 0.097
11 7.5 0.500 0.36 6.1 0.071
12 5.6 0.615 0.00 1.6 0.089
13 7.8 0.610 0.29 1.6 0.114
14 8.9 0.620 0.18 3.8 0.176
15 8.9 0.620 0.19 3.9 0.170
16 8.5 0.280 0.56 1.8 0.092
17 8.1 0.560 0.28 1.7 0.368
18 7.4 0.590 0.08 4.4 0.086
19 7.9 0.320 0.51 1.8 0.341
20 8.9 0.220 0.48 1.8 0.077
21 7.6 0.390 0.31 2.3 0.082
22 7.9 0.430 0.21 1.6 0.106
23 8.5 0.490 0.11 2.3 0.084
24 6.9 0.400 0.14 2.4 0.085
25 6.3 0.390 0.16 1.4 0.080
26 7.6 0.410 0.24 1.8 0.080
27 7.9 0.430 0.21 1.6 0.106
28 7.1 0.710 0.00 1.9 0.080
29 7.8 0.645 0.00 2.0 0.082
... ... ... ... ... ...
1569 6.2 0.510 0.14 1.9 0.056
1570 6.4 0.360 0.53 2.2 0.230
1571 6.4 0.380 0.14 2.2 0.038
1572 7.3 0.690 0.32 2.2 0.069
1573 6.0 0.580 0.20 2.4 0.075
1574 5.6 0.310 0.78 13.9 0.074
1575 7.5 0.520 0.40 2.2 0.060
1576 8.0 0.300 0.63 1.6 0.081
1577 6.2 0.700 0.15 5.1 0.076
1578 6.8 0.670 0.15 1.8 0.118
1579 6.2 0.560 0.09 1.7 0.053
1580 7.4 0.350 0.33 2.4 0.068
1581 6.2 0.560 0.09 1.7 0.053
1582 6.1 0.715 0.10 2.6 0.053
1583 6.2 0.460 0.29 2.1 0.074
1584 6.7 0.320 0.44 2.4 0.061
1585 7.2 0.390 0.44 2.6 0.066
1586 7.5 0.310 0.41 2.4 0.065
1587 5.8 0.610 0.11 1.8 0.066
1588 7.2 0.660 0.33 2.5 0.068
1589 6.6 0.725 0.20 7.8 0.073
1590 6.3 0.550 0.15 1.8 0.077
1591 5.4 0.740 0.09 1.7 0.089
1592 6.3 0.510 0.13 2.3 0.076
1593 6.8 0.620 0.08 1.9 0.068
1594 6.2 0.600 0.08 2.0 0.090
1595 5.9 0.550 0.10 2.2 0.062
1596 6.3 0.510 0.13 2.3 0.076
1597 5.9 0.645 0.12 2.0 0.075
1598 6.0 0.310 0.47 3.6 0.067
free sulfur dioxide total sulfur dioxide density pH sulphates \
0 11.0 34.0 0.99780 3.51 0.56
1 25.0 67.0 0.99680 3.20 0.68
2 15.0 54.0 0.99700 3.26 0.65
3 17.0 60.0 0.99800 3.16 0.58
4 11.0 34.0 0.99780 3.51 0.56
5 13.0 40.0 0.99780 3.51 0.56
6 15.0 59.0 0.99640 3.30 0.46
7 15.0 21.0 0.99460 3.39 0.47
8 9.0 18.0 0.99680 3.36 0.57
9 17.0 102.0 0.99780 3.35 0.80
10 15.0 65.0 0.99590 3.28 0.54
11 17.0 102.0 0.99780 3.35 0.80
12 16.0 59.0 0.99430 3.58 0.52
13 9.0 29.0 0.99740 3.26 1.56
14 52.0 145.0 0.99860 3.16 0.88
15 51.0 148.0 0.99860 3.17 0.93
16 35.0 103.0 0.99690 3.30 0.75
17 16.0 56.0 0.99680 3.11 1.28
18 6.0 29.0 0.99740 3.38 0.50
19 17.0 56.0 0.99690 3.04 1.08
20 29.0 60.0 0.99680 3.39 0.53
21 23.0 71.0 0.99820 3.52 0.65
22 10.0 37.0 0.99660 3.17 0.91
23 9.0 67.0 0.99680 3.17 0.53
24 21.0 40.0 0.99680 3.43 0.63
25 11.0 23.0 0.99550 3.34 0.56
26 4.0 11.0 0.99620 3.28 0.59
27 10.0 37.0 0.99660 3.17 0.91
28 14.0 35.0 0.99720 3.47 0.55
29 8.0 16.0 0.99640 3.38 0.59
... ... ... ... ... ...
1569 15.0 34.0 0.99396 3.48 0.57
1570 19.0 35.0 0.99340 3.37 0.93
1571 15.0 25.0 0.99514 3.44 0.65
1572 35.0 104.0 0.99632 3.33 0.51
1573 15.0 50.0 0.99467 3.58 0.67
1574 23.0 92.0 0.99677 3.39 0.48
1575 12.0 20.0 0.99474 3.26 0.64
1576 16.0 29.0 0.99588 3.30 0.78
1577 13.0 27.0 0.99622 3.54 0.60
1578 13.0 20.0 0.99540 3.42 0.67
1579 24.0 32.0 0.99402 3.54 0.60
1580 9.0 26.0 0.99470 3.36 0.60
1581 24.0 32.0 0.99402 3.54 0.60
1582 13.0 27.0 0.99362 3.57 0.50
1583 32.0 98.0 0.99578 3.33 0.62
1584 24.0 34.0 0.99484 3.29 0.80
1585 22.0 48.0 0.99494 3.30 0.84
1586 34.0 60.0 0.99492 3.34 0.85
1587 18.0 28.0 0.99483 3.55 0.66
1588 34.0 102.0 0.99414 3.27 0.78
1589 29.0 79.0 0.99770 3.29 0.54
1590 26.0 35.0 0.99314 3.32 0.82
1591 16.0 26.0 0.99402 3.67 0.56
1592 29.0 40.0 0.99574 3.42 0.75
1593 28.0 38.0 0.99651 3.42 0.82
1594 32.0 44.0 0.99490 3.45 0.58
1595 39.0 51.0 0.99512 3.52 0.76
1596 29.0 40.0 0.99574 3.42 0.75
1597 32.0 44.0 0.99547 3.57 0.71
1598 18.0 42.0 0.99549 3.39 0.66
alcohol quality
0 9.4 5
1 9.8 5
2 9.8 5
3 9.8 6
4 9.4 5
5 9.4 5
6 9.4 5
7 10.0 7
8 9.5 7
9 10.5 5
10 9.2 5
11 10.5 5
12 9.9 5
13 9.1 5
14 9.2 5
15 9.2 5
16 10.5 7
17 9.3 5
18 9.0 4
19 9.2 6
20 9.4 6
21 9.7 5
22 9.5 5
23 9.4 5
24 9.7 6
25 9.3 5
26 9.5 5
27 9.5 5
28 9.4 5
29 9.8 6
... ... ...
1569 11.5 6
1570 12.4 6
1571 11.1 6
1572 9.5 5
1573 12.5 6
1574 10.5 6
1575 11.8 6
1576 10.8 6
1577 11.9 6
1578 11.3 6
1579 11.3 5
1580 11.9 6
1581 11.3 5
1582 11.9 5
1583 9.8 5
1584 11.6 7
1585 11.5 6
1586 11.4 6
1587 10.9 6
1588 12.8 6
1589 9.2 5
1590 11.6 6
1591 11.6 6
1592 11.0 6
1593 9.5 6
1594 10.5 5
1595 11.2 6
1596 11.0 6
1597 10.2 5
1598 11.0 6
[1599 rows x 12 columns]>
<bound method DataFrame.info of fixed acidity volatile acidity citric acid residual sugar chlorides \
0 7.0 0.270 0.36 20.70 0.045
1 6.3 0.300 0.34 1.60 0.049
2 8.1 0.280 0.40 6.90 0.050
3 7.2 0.230 0.32 8.50 0.058
4 7.2 0.230 0.32 8.50 0.058
5 8.1 0.280 0.40 6.90 0.050
6 6.2 0.320 0.16 7.00 0.045
7 7.0 0.270 0.36 20.70 0.045
8 6.3 0.300 0.34 1.60 0.049
9 8.1 0.220 0.43 1.50 0.044
10 8.1 0.270 0.41 1.45 0.033
11 8.6 0.230 0.40 4.20 0.035
12 7.9 0.180 0.37 1.20 0.040
13 6.6 0.160 0.40 1.50 0.044
14 8.3 0.420 0.62 19.25 0.040
15 6.6 0.170 0.38 1.50 0.032
16 6.3 0.480 0.04 1.10 0.046
17 6.2 0.660 0.48 1.20 0.029
18 7.4 0.340 0.42 1.10 0.033
19 6.5 0.310 0.14 7.50 0.044
20 6.2 0.660 0.48 1.20 0.029
21 6.4 0.310 0.38 2.90 0.038
22 6.8 0.260 0.42 1.70 0.049
23 7.6 0.670 0.14 1.50 0.074
24 6.6 0.270 0.41 1.30 0.052
25 7.0 0.250 0.32 9.00 0.046
26 6.9 0.240 0.35 1.00 0.052
27 7.0 0.280 0.39 8.70 0.051
28 7.4 0.270 0.48 1.10 0.047
29 7.2 0.320 0.36 2.00 0.033
... ... ... ... ... ...
4868 5.8 0.230 0.31 4.50 0.046
4869 6.6 0.240 0.33 10.10 0.032
4870 6.1 0.320 0.28 6.60 0.021
4871 5.0 0.200 0.40 1.90 0.015
4872 6.0 0.420 0.41 12.40 0.032
4873 5.7 0.210 0.32 1.60 0.030
4874 5.6 0.200 0.36 2.50 0.048
4875 7.4 0.220 0.26 1.20 0.035
4876 6.2 0.380 0.42 2.50 0.038
4877 5.9 0.540 0.00 0.80 0.032
4878 6.2 0.530 0.02 0.90 0.035
4879 6.6 0.340 0.40 8.10 0.046
4880 6.6 0.340 0.40 8.10 0.046
4881 5.0 0.235 0.27 11.75 0.030
4882 5.5 0.320 0.13 1.30 0.037
4883 4.9 0.470 0.17 1.90 0.035
4884 6.5 0.330 0.38 8.30 0.048
4885 6.6 0.340 0.40 8.10 0.046
4886 6.2 0.210 0.28 5.70 0.028
4887 6.2 0.410 0.22 1.90 0.023
4888 6.8 0.220 0.36 1.20 0.052
4889 4.9 0.235 0.27 11.75 0.030
4890 6.1 0.340 0.29 2.20 0.036
4891 5.7 0.210 0.32 0.90 0.038
4892 6.5 0.230 0.38 1.30 0.032
4893 6.2 0.210 0.29 1.60 0.039
4894 6.6 0.320 0.36 8.00 0.047
4895 6.5 0.240 0.19 1.20 0.041
4896 5.5 0.290 0.30 1.10 0.022
4897 6.0 0.210 0.38 0.80 0.020
free sulfur dioxide total sulfur dioxide density pH sulphates \
0 45.0 170.0 1.00100 3.00 0.45
1 14.0 132.0 0.99400 3.30 0.49
2 30.0 97.0 0.99510 3.26 0.44
3 47.0 186.0 0.99560 3.19 0.40
4 47.0 186.0 0.99560 3.19 0.40
5 30.0 97.0 0.99510 3.26 0.44
6 30.0 136.0 0.99490 3.18 0.47
7 45.0 170.0 1.00100 3.00 0.45
8 14.0 132.0 0.99400 3.30 0.49
9 28.0 129.0 0.99380 3.22 0.45
10 11.0 63.0 0.99080 2.99 0.56
11 17.0 109.0 0.99470 3.14 0.53
12 16.0 75.0 0.99200 3.18 0.63
13 48.0 143.0 0.99120 3.54 0.52
14 41.0 172.0 1.00020 2.98 0.67
15 28.0 112.0 0.99140 3.25 0.55
16 30.0 99.0 0.99280 3.24 0.36
17 29.0 75.0 0.98920 3.33 0.39
18 17.0 171.0 0.99170 3.12 0.53
19 34.0 133.0 0.99550 3.22 0.50
20 29.0 75.0 0.98920 3.33 0.39
21 19.0 102.0 0.99120 3.17 0.35
22 41.0 122.0 0.99300 3.47 0.48
23 25.0 168.0 0.99370 3.05 0.51
24 16.0 142.0 0.99510 3.42 0.47
25 56.0 245.0 0.99550 3.25 0.50
26 35.0 146.0 0.99300 3.45 0.44
27 32.0 141.0 0.99610 3.38 0.53
28 17.0 132.0 0.99140 3.19 0.49
29 37.0 114.0 0.99060 3.10 0.71
... ... ... ... ... ...
4868 42.0 124.0 0.99324 3.31 0.64
4869 8.0 81.0 0.99626 3.19 0.51
4870 29.0 132.0 0.99188 3.15 0.36
4871 20.0 98.0 0.98970 3.37 0.55
4872 50.0 179.0 0.99622 3.14 0.60
4873 33.0 122.0 0.99044 3.33 0.52
4874 16.0 125.0 0.99282 3.49 0.49
4875 18.0 97.0 0.99245 3.12 0.41
4876 34.0 117.0 0.99132 3.36 0.59
4877 12.0 82.0 0.99286 3.25 0.36
4878 6.0 81.0 0.99234 3.24 0.35
4879 68.0 170.0 0.99494 3.15 0.50
4880 68.0 170.0 0.99494 3.15 0.50
4881 34.0 118.0 0.99540 3.07 0.50
4882 45.0 156.0 0.99184 3.26 0.38
4883 60.0 148.0 0.98964 3.27 0.35
4884 68.0 174.0 0.99492 3.14 0.50
4885 68.0 170.0 0.99494 3.15 0.50
4886 45.0 121.0 0.99168 3.21 1.08
4887 5.0 56.0 0.98928 3.04 0.79
4888 38.0 127.0 0.99330 3.04 0.54
4889 34.0 118.0 0.99540 3.07 0.50
4890 25.0 100.0 0.98938 3.06 0.44
4891 38.0 121.0 0.99074 3.24 0.46
4892 29.0 112.0 0.99298 3.29 0.54
4893 24.0 92.0 0.99114 3.27 0.50
4894 57.0 168.0 0.99490 3.15 0.46
4895 30.0 111.0 0.99254 2.99 0.46
4896 20.0 110.0 0.98869 3.34 0.38
4897 22.0 98.0 0.98941 3.26 0.32
alcohol quality
0 8.800000 6
1 9.500000 6
2 10.100000 6
3 9.900000 6
4 9.900000 6
5 10.100000 6
6 9.600000 6
7 8.800000 6
8 9.500000 6
9 11.000000 6
10 12.000000 5
11 9.700000 5
12 10.800000 5
13 12.400000 7
14 9.700000 5
15 11.400000 7
16 9.600000 6
17 12.800000 8
18 11.300000 6
19 9.500000 5
20 12.800000 8
21 11.000000 7
22 10.500000 8
23 9.300000 5
24 10.000000 6
25 10.400000 6
26 10.000000 6
27 10.500000 6
28 11.600000 6
29 12.300000 7
... ... ...
4868 10.800000 6
4869 9.800000 6
4870 11.450000 7
4871 12.050000 6
4872 9.700000 5
4873 11.900000 6
4874 10.000000 6
4875 9.700000 6
4876 11.600000 7
4877 8.800000 5
4878 9.500000 4
4879 9.533333 6
4880 9.533333 6
4881 9.400000 6
4882 10.700000 5
4883 11.500000 6
4884 9.600000 5
4885 9.550000 6
4886 12.150000 7
4887 13.000000 7
4888 9.200000 5
4889 9.400000 6
4890 11.800000 6
4891 10.600000 6
4892 9.700000 5
4893 11.200000 6
4894 9.600000 5
4895 9.400000 6
4896 12.800000 7
4897 11.800000 6
[4898 rows x 12 columns]>
在读取数据集时,红酒和白酒是分别存在于两个DataFrame变量中的,为了方便分类任务,需要将两个变量进行合并。下面对数据作预处理,然后就可以开始搭建自己的神经网络了。
|
|
协方差矩阵
现在我们已经有了完整数据集,可以再做一些更深入的数据挖掘。协方差矩阵图像就是一种很好的方法,可以直观地展示变量之间的相关性:
|
|

训练集与测试集
大多数分类数据,都不是每个类别的样本恰好一样多,这种不平衡就会导致一些分类上的问题。(比如一个数据集里,两个类别的数量比例是7:3,那只要算法全部猜测为多的那一类,也能得到70%的正确率。)这样我们就需要让两个类别的酒都在训练集里出现,而且数量要基本一致,这样才不会产生偏差。
酒质量的这个数据及就是不平衡的,但我们先不做额外处理,之后可以再衡量分类性能是否有所下降,借助下采样或上采样等方式。现在,先导入sklearn.model_selection里的train_test_split方法,来把数据和标签分配到变量X和y当中。我们还需要调用ravel()函数把数据“展平”,以适应之后的函数输入格式。
|
|
至此我们已经准备好构建第一个神经网络了,但是还有一件事值得留意,那就是数据的标准化。
数据标准化
当有些数据值相隔甚远的时候,就需要进行标准化处理。Scikit-Learn提供了很强力且快捷的方式:从sklearn.preprocessing模块导入StandardScaler工具:
|
|
搭建神经网络
在真正开始建模之前,回顾我们一开始的问题:能否根据化学性质,如挥发性酸度或硫酸盐,预测酒是红酒还是白酒?因为这里有两个分类:红or白,所以是个二分类(binary classification)问题,本质上相当于0/1, yes/no。因为神经网络只能处理数值信息,所以之前已经将红/白编码成了0/1。
多层感知器是一种擅长二分类的神经网络,在本教程开头已经介绍过,多层感知器通常是全连接的,也就是简单地把若干全连接层堆砌起来。在激活函数的选择上,基于熟悉Keras和神经网络的目的,可以使用最最普遍的ReLU函数。
那么如何开始着手构建呢?一个快捷的方法是使用Keras的序贯模型(Sequential model):层的线性堆叠。我们可以轻松地创建模型,再把层实例传递给模型,具体的命令是:model=Sequential()。
现在来想一想多层感知器的结构:输入层,若干隐藏层和输出层。当你构建自己的模型时,必须清楚定义输入形状,模型需要知道输入形状,所以你会发现input_shape, input_dim, input_length或batch_size等。
全连接层在Keras里称为Dense层,执行了以下操作output = activation(dot(inputs, units) + bias)。注意如果没有激活函数的话,Dense层就只包含两个线性操作:点乘、求和。
在第一层当中,activation参数取值relu,之后定义了input_shape=(11, ),因为有11个特征。第一个隐藏层含有16个神经元,所以Dense()的units参数等于16,也就是说模型的输出形状为(*, 16)。units代表的就是权重矩阵,内有对应每个输入节点的权重值。因为没有将use_bias设为TRUE,所以暂时没有偏置项,这也是可行的。
第二个隐藏层同样使用relu激活函数,这层的输出数组形状为(*, 8)。最后的输出Dense层尺寸为1,用sigmoid激活函数,所以最终的输出结果是一个0-1之间的概率,对应的是样本属于标签1,即红酒的概率。
请在下方的代码区域搭建神经网络,要求:
- 使用Sequential()模型
- 共有3层,且第一层的输入参数为(11,)
- 输出层使用sigmoid激活函数
|
|
Using TensorFlow backend.
总的来讲,关于神经网络的架构,有两个关键的决策:
- 多少层?
- 每层多少个单元?
在这个例子中,我们第一层有16个单元,也就是在学习数据表征时的自由度,更多的隐藏单元可以学习更复杂的表征,但是计算消耗也更大,而且容易过拟合(overfitting)。当模型过于复杂的时候,就会出现过拟合:把一些随机的误差或噪音也当作特征,换言之就是训练数据被拟合的“太好了”。所以当我们并没有足够多数据的时候,最好还是用相对小的神经网络,层数也不要太多。
如果想要获取所建模型的信息,可以使用output_shape或summary()函数,喜爱main列举了几种常用方法:
|
|
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 16) 192
_________________________________________________________________
dense_2 (Dense) (None, 8) 136
_________________________________________________________________
dense_3 (Dense) (None, 1) 9
=================================================================
Total params: 337
Trainable params: 337
Non-trainable params: 0
_________________________________________________________________
[array([[ -4.98264432e-02, -8.99875760e-02, 1.66897923e-01,
3.89293462e-01, 2.48389035e-01, 1.94905251e-01,
3.81554663e-02, -1.70459509e-01, -4.62478936e-01,
9.45781171e-02, -9.45084095e-02, 4.50080931e-02,
-2.01654226e-01, -2.18820870e-02, -3.53524268e-01,
-3.39704037e-01],
[ 4.67661113e-01, 6.37504160e-02, -2.29388103e-01,
-5.40849864e-02, 2.22171873e-01, 2.39076287e-01,
-3.60502452e-01, -3.84893119e-01, 1.26932710e-01,
3.79719436e-02, 3.56621891e-01, 1.69539779e-01,
4.34244841e-01, 4.50510353e-01, 2.42370367e-02,
-2.50114679e-01],
[ -3.73600125e-01, -2.06571698e-01, -1.06325597e-01,
1.82575583e-02, 9.36785340e-03, -7.66809583e-02,
3.23935062e-01, 3.03234130e-01, 1.04181617e-01,
-3.18242192e-01, 2.15769619e-01, -2.10983753e-02,
1.22898072e-01, 3.79836261e-02, -2.06408739e-01,
1.86543435e-01],
[ -1.59280300e-02, 2.84385353e-01, -1.80770189e-01,
-6.91838861e-02, -4.28074747e-01, -3.27124178e-01,
1.92455947e-02, 4.65576321e-01, 2.14139491e-01,
2.47457176e-01, 9.40738022e-02, -2.64835954e-01,
-3.01520914e-01, -2.66410232e-01, 2.50897020e-01,
-2.39203826e-01],
[ 9.09360349e-02, -2.52071738e-01, 1.81674153e-01,
4.17934448e-01, -4.57543045e-01, 4.53864366e-01,
1.57245368e-01, -3.64349395e-01, 3.86538893e-01,
-1.76164597e-01, -5.79869747e-02, -2.85525113e-01,
-1.39552027e-01, 5.49268723e-03, -3.44688624e-01,
-2.01445311e-01],
[ -3.61947805e-01, -4.36158180e-02, 2.21010417e-01,
-4.11448449e-01, 1.11243278e-01, -1.96210444e-01,
-3.63108486e-01, 3.47647637e-01, 7.67233074e-02,
-4.12058502e-01, -2.14669198e-01, -3.62275094e-01,
-1.37348175e-02, 1.43671960e-01, -1.09374881e-01,
-1.29260212e-01],
[ 1.84318751e-01, 1.69243068e-01, 2.64439911e-01,
-3.27584505e-01, -3.12709033e-01, 2.97704428e-01,
1.93249792e-01, 2.26672620e-01, -2.32822448e-01,
-3.53965074e-01, 3.30718786e-01, 8.20287764e-02,
1.41222507e-01, -4.48238492e-01, -1.47753030e-01,
-4.31054354e-01],
[ -3.64983499e-01, 2.66292900e-01, 8.03867280e-02,
-3.78615826e-01, -3.46475422e-01, 1.89222127e-01,
2.69394010e-01, 2.37171561e-01, -3.25533509e-01,
3.10469061e-01, 1.54059440e-01, 4.10036236e-01,
3.57707292e-01, -4.47573662e-02, -3.61494094e-01,
2.87418455e-01],
[ -3.18877876e-01, 2.47041434e-01, -2.29884654e-01,
8.18514526e-02, 2.36380666e-01, -3.12529325e-01,
2.58298367e-01, -3.12896848e-01, 4.36720461e-01,
8.30825865e-02, -1.53442502e-01, 2.92674035e-01,
2.43945867e-01, -3.45032215e-01, 9.18445289e-02,
-2.73343891e-01],
[ 1.14024431e-01, -1.97158337e-01, 2.65030652e-01,
-3.90317142e-01, -5.33969104e-02, -1.00827187e-01,
1.35453552e-01, -2.08345950e-02, -3.05458009e-01,
3.28467578e-01, 3.91551107e-01, 3.88602704e-01,
4.19867784e-01, 1.98601454e-01, -2.90410578e-01,
2.18321770e-01],
[ 3.94538552e-01, -3.01331282e-04, -4.59927320e-01,
3.52448225e-03, -2.55332798e-01, -7.66898394e-02,
1.71944499e-02, 2.51493305e-01, -6.00979328e-02,
4.07272190e-01, -1.14112884e-01, -4.47229087e-01,
-1.85045898e-02, 2.91900188e-01, 4.34516460e-01,
-3.59144658e-01]], dtype=float32),
array([ 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
0., 0., 0.], dtype=float32),
array([[ 0.27758062, 0.32696116, -0.12059772, -0.2686069 , 0.08139598,
0.38036656, 0.32520974, 0.19151318],
[ 0.43766093, 0.29809725, -0.4557929 , -0.18581784, 0.08751357,
-0.39931965, -0.09964991, 0.17332137],
[-0.2620455 , -0.24762535, 0.35845268, -0.13336289, 0.04007018,
-0.39839149, 0.01755929, 0.11646259],
[-0.28185141, -0.41674638, 0.07205951, 0.46127093, 0.42340422,
-0.12234998, -0.32808745, 0.49965596],
[-0.26166177, -0.4406935 , 0.3176899 , 0.32351041, -0.06424642,
0.41437888, 0.36301064, 0.2036624 ],
[-0.27416241, -0.35417187, 0.26924002, 0.32288253, -0.16948187,
-0.35796487, -0.04283953, -0.44096291],
[-0.01216853, -0.30725086, -0.38324308, 0.19532835, -0.30979538,
0.18932819, 0.26240873, -0.4475528 ],
[-0.1612885 , 0.19788098, -0.19374907, -0.06785023, 0.21359551,
0.3040458 , 0.39540446, 0.23423409],
[ 0.01686943, 0.07593989, 0.00735629, 0.25039053, 0.25843036,
-0.23249888, 0.02778065, -0.30911994],
[-0.1596216 , -0.25759542, -0.19575047, -0.02004528, 0.22266507,
-0.1529597 , -0.2789892 , 0.12094378],
[ 0.19889224, 0.44975781, 0.11675143, -0.16397417, 0.25484574,
0.36306274, 0.48795998, 0.47419429],
[-0.45383811, 0.13647282, -0.2559135 , 0.05184174, 0.02903581,
0.17449057, -0.27694225, 0.13545072],
[ 0.29954553, 0.2175715 , -0.04698312, 0.05174255, 0.25326657,
0.12707448, -0.45172453, 0.41674447],
[-0.34929419, 0.17539358, 0.35529578, 0.26315773, -0.06466413,
-0.19027662, -0.204934 , -0.33771062],
[-0.30182111, -0.01916206, -0.07562017, -0.34805727, -0.27742755,
0.18699825, -0.30500996, -0.43830144],
[-0.45377958, -0.09787893, 0.16146803, -0.07033706, -0.08875155,
0.04072464, -0.32710898, -0.18625259]], dtype=float32),
array([ 0., 0., 0., 0., 0., 0., 0., 0.], dtype=float32),
array([[-0.47236764],
[-0.39696497],
[ 0.32774436],
[ 0.39144981],
[-0.42509505],
[-0.5582419 ],
[ 0.58168077],
[ 0.20806301]], dtype=float32),
array([ 0.], dtype=float32)]
编译和拟合
现在是时候编译我们的模型并针对数据进行拟合了,相应的函数是compile()和fit():
|
|
Epoch 1/5
3s - loss: 0.0807 - acc: 0.9809
Epoch 2/5
3s - loss: 0.0291 - acc: 0.9949
Epoch 3/5
3s - loss: 0.0239 - acc: 0.9959
Epoch 4/5
3s - loss: 0.0211 - acc: 0.9961
Epoch 5/5
3s - loss: 0.0187 - acc: 0.9966
<keras.callbacks.History at 0x2aebe9a4d68>
在编译(compile)过程中,我们为模型指定了adam优化器和binary_crossentropy损失函数。将['accuracy']传给参数metrics还可以监测训练过程中的准确度。optimizer和loss是编译模型需要的另外两个参数,最流行的几种优化算法有:随即梯度下降(Stochastic Gradient Descent, SGD),ADAM和RMSprop。根据所选算法不同,调整的参数也会有不同,不如学习率或者动量(momentum)。损失函数的选择取决于面对的任务:比如回归问题一般用均方误差(Mean Squared Error, MSE)。而在这个二分类的例子中,我们用binary_crossentropy;对于多分类任务,可以使用categorical_crossentropy。
之后我们对所有X_train和y_train的样本迭代训练了5个来回,批次规模为1个样本。verbose则是为了设置输出内容。我们用特定的迭代回数训练模型,一次迭代(epoch)就是把所有训练集筛过一遍,然后对照测试集。批规模(batch size)则定义了每次在网络里传播的样本数量,这样做也是为了在内存有限的情况下优化效率。
预测值
下面把训练的模型投入实战,你可以对测试集数据,预测每个样本的标签,只需调用predict(),把结果赋值给变量y_pred:
|
|
评价模型
现在我们已经建立了模型,并且用于对此前未见的数据做预测,之后肯定还要衡量平价一下整个模型的表现。可以直接拿y_pred和y_test去比较看看中了几个,或者使用其他更高级的度量衡。对这个实例,我们调用evaluate()函数,传递测试数据+测试标签即可得到全局得分:
|
|
[0.022412170111003608, 0.9944055944055944]