文中主要总结动态规划的01背包问题以及相关实例，然后通过c++解决问题

一、背包问题

01背包问题

题目

有N件物品和一个容积为V的背包。第i件物品的体积是c[i]，价值是w[i]。求解将哪些物品装入背包可使价值总和最大。

基本思路

这是最基础的背包问题，特点是：每种物品仅有一件，可以选择放或不放。
用子问题定义状态：即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。则其状态转移方程便是：

• 二维方程：f[i][v]=max(f[i-1][v],f[i-1][v-c[i]]+w[i])
• 一维方程：f[v]=max(f[v],f[v-c[i]]+w[i])
  状态转移方程解释：“将前i件物品放入容量为v的背包中”这个子问题，若只考虑第i件物品放或不放，那么就可以转化为一个只牵扯前i-1件物品的问题。如果不放第i件物品，那么问题就转化为“前i-1件物品放入容量为v的背包中”，价值为f[i-1][v]；如果放第i件物品，那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”，此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。

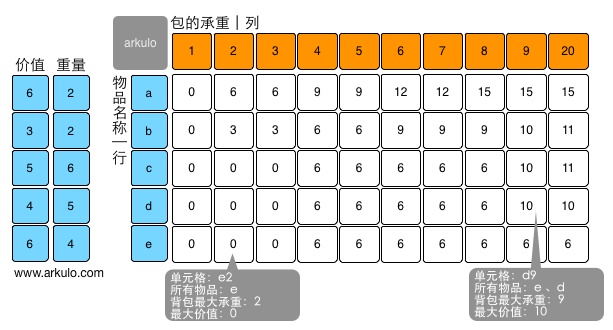
图解

参考

有了这张图和上面总结的公式，我们就可以很清晰的理解01背包算法了

1. e2单元格：当只有一件物品e，包的容量是2时，装不进去，所以最大值为0
2. a8单元格：物品包括a、b、c、d、e，容量为8时，F[i-1,j]=F[b,8]=9，F[i-1,j-Wi]+Pi=F[b,6]+6=9+6=15，两种情况取最大值，因此这里的最大值是15

##实例1 采药(RQNOJ15)；

题目描述

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”
　　如果你是辰辰，你能完成这个任务吗？

输入格式

　输入的第一行有两个整数T（1 <= T <= 1000）和M（1 <= M <= 100），用一个空格隔开，T代表总共能够用来采药的时间，M代表山洞里的草药的数目。接下来的M行每行包括两个在1到100之间（包括1和100）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出格式

输出包括一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

样例输入：

70 3
71 100
69 1
1 2

样例输出：

3

参考程序1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

#include<iostream>
using namespace std;
int ti[101],money[101];
int f[1001];
int main(){
    int t,m,i,j;
    cin>>t>>m;
    for(i=1;i<=m;i++){
        cin>>ti[i]>>money[i];
    }
    for(i=1;i<=m;i++){
        for(j=t;j>=ti[i];j--){
            if(f[j-ti[i]]+money[i]>f[j]){//把最大值赋值给f[t]
                f[j]=f[j-ti[i]]+money[i];
            }
        }
    }
    cout<<f[t];
}

参考程序2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include<iostream>
using namespace std;
#define  V 1500
unsigned int f[10][V];//全局变量，自动初始化为0
unsigned int weight[10];
unsigned int value[10];
#define  max(x,y)   (x)>(y)?(x):(y)
int main()
{
    int N,M;
    cin>>M;//背包容量
    cin>>N;//药品个数
    for (int i=1;i<=N; i++)
    {
        cin>>weight[i]>>value[i];
    }
    for (int i=1; i<=N; i++)
        for (int j=1; j<=M; j++)
        {
            if (weight[i]<=j)
            {
                f[i][j]=max(f[i-1][j],f[i-1][j-weight[i]]+value[i]);
            }
            else
                f[i][j]=f[i-1][j];
        }
    cout<<f[N][M]<<endl;//输出最优解
}