Planar data classification with one hidden layer
Welcome to your week 3 programming assignment. It’s time to build your first neural network, which will have a hidden layer. You will see a big difference between this model and the one you implemented using logistic regression.
You will learn how to:
- Implement a 2-class classification neural network with a single hidden layer
- Use units with a non-linear activation function, such as tanh
- Compute the cross entropy loss
- Implement forward and backward propagation
1 - Packages
Let’s first import all the packages that you will need during this assignment.
- numpy is the fundamental package for scientific computing with Python.
- sklearn provides simple and efficient tools for data mining and data analysis.
- matplotlib is a library for plotting graphs in Python.
- testCases provides some test examples to assess the correctness of your functions
- planar_utils provide various useful functions used in this assignment
|
|
2 - Dataset
First, let’s get the dataset you will work on. The following code will load a “flower” 2-class dataset into variables X and Y.
|
|
Visualize the dataset using matplotlib. The data looks like a “flower” with some red (label y=0) and some blue (y=1) points. Your goal is to build a model to fit this data.
|
|
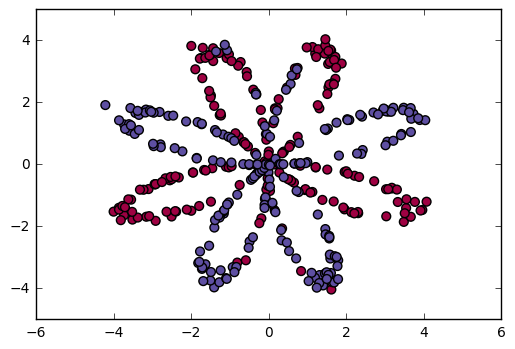
You have:
- a numpy-array (matrix) X that contains your features (x1, x2)
- a numpy-array (vector) Y that contains your labels (red:0, blue:1).
Lets first get a better sense of what our data is like.
Exercise: How many training examples do you have? In addition, what is the shape of the variables X and Y?
Hint: How do you get the shape of a numpy array? (help)
|
|
The shape of X is: (2, 400)
The shape of Y is: (1, 400)
I have m = 400 training examples!
Expected Output:
| shape of X | (2, 400) |
| shape of Y | (1, 400) |
| m | 400 |
3 - Simple Logistic Regression
Before building a full neural network, lets first see how logistic regression performs on this problem. You can use sklearn’s built-in functions to do that. Run the code below to train a logistic regression classifier on the dataset.
|
|
/opt/conda/lib/python3.5/site-packages/sklearn/utils/validation.py:515: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
y = column_or_1d(y, warn=True)
You can now plot the decision boundary of these models. Run the code below.
|
|
Accuracy of logistic regression: 47 % (percentage of correctly labelled datapoints)
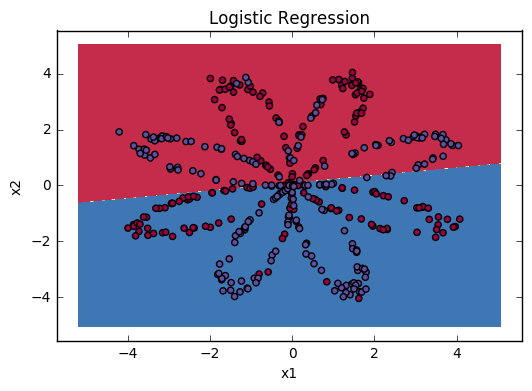
Expected Output:
| Accuracy | 47% |
Interpretation: The dataset is not linearly separable, so logistic regression doesn’t perform well. Hopefully a neural network will do better. Let’s try this now!
4 - Neural Network model
Logistic regression did not work well on the “flower dataset”. You are going to train a Neural Network with a single hidden layer.
Here is our model:
Mathematically:
For one example $x^{(i)}$:
$$z^{[1] (i)} = W^{[1]} x^{(i)} + b^{[1] (i)}\tag{1}$$
$$a^{[1] (i)} = \tanh(z^{[1] (i)})\tag{2}$$
$$z^{[2] (i)} = W^{[2]} a^{[1] (i)} + b^{[2] (i)}\tag{3}$$
$$\hat{y}^{(i)} = a^{[2] (i)} = \sigma(z^{ [2] (i)})\tag{4}$$
$$y^{(i)}_{prediction} = \begin{cases} 1 & \mbox{if } a^{2} > 0.5 \ 0 & \mbox{otherwise } \end{cases}\tag{5}$$
Given the predictions on all the examples, you can also compute the cost $J$ as follows:
$$J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large\left(\small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large \right) \small \tag{6}$$
Reminder: The general methodology to build a Neural Network is to:
1. Define the neural network structure ( # of input units, # of hidden units, etc).
2. Initialize the model's parameters
3. Loop:
- Implement forward propagation
- Compute loss
- Implement backward propagation to get the gradients
- Update parameters (gradient descent)
You often build helper functions to compute steps 1-3 and then merge them into one function we call nn_model(). Once you’ve built nn_model() and learnt the right parameters, you can make predictions on new data.
4.1 - Defining the neural network structure
Exercise: Define three variables:
- n_x: the size of the input layer
- n_h: the size of the hidden layer (set this to 4)
- n_y: the size of the output layer
Hint: Use shapes of X and Y to find n_x and n_y. Also, hard code the hidden layer size to be 4.
|
|
|
|
The size of the input layer is: n_x = 5
The size of the hidden layer is: n_h = 4
The size of the output layer is: n_y = 2
Expected Output (these are not the sizes you will use for your network, they are just used to assess the function you’ve just coded).
| n_x | 5 |
| n_h | 4 |
| n_y | 2 |
4.2 - Initialize the model’s parameters
Exercise: Implement the function initialize_parameters().
Instructions:
- Make sure your parameters’ sizes are right. Refer to the neural network figure above if needed.
- You will initialize the weights matrices with random values.
- Use:
np.random.randn(a,b) * 0.01to randomly initialize a matrix of shape (a,b).
- Use:
- You will initialize the bias vectors as zeros.
- Use:
np.zeros((a,b))to initialize a matrix of shape (a,b) with zeros.
- Use:
|
|
|
|
W1 = [[-0.00416758 -0.00056267]
[-0.02136196 0.01640271]
[-0.01793436 -0.00841747]
[ 0.00502881 -0.01245288]]
b1 = [[ 0.]
[ 0.]
[ 0.]
[ 0.]]
W2 = [[-0.01057952 -0.00909008 0.00551454 0.02292208]]
b2 = [[ 0.]]
Expected Output:
| W1 | [[-0.00416758 -0.00056267] [-0.02136196 0.01640271] [-0.01793436 -0.00841747] [ 0.00502881 -0.01245288]] |
| b1 | [[ 0.] [ 0.] [ 0.] [ 0.]] |
| W2 | [[-0.01057952 -0.00909008 0.00551454 0.02292208]] |
| b2 | [[ 0.]] |
4.3 - The Loop
Question: Implement forward_propagation().
Instructions:
- Look above at the mathematical representation of your classifier.
- You can use the function
sigmoid(). It is built-in (imported) in the notebook. - You can use the function
np.tanh(). It is part of the numpy library. - The steps you have to implement are:
- Retrieve each parameter from the dictionary “parameters” (which is the output of
initialize_parameters()) by usingparameters[".."]. - Implement Forward Propagation. Compute $Z^{[1]}, A^{[1]}, Z^{[2]}$ and $A^{[2]}$ (the vector of all your predictions on all the examples in the training set).
- Retrieve each parameter from the dictionary “parameters” (which is the output of
- Values needed in the backpropagation are stored in “
cache“. Thecachewill be given as an input to the backpropagation function.
|
|
|
|
-0.000499755777742 -0.000496963353232 0.000438187450959 0.500109546852
Expected Output:
| -0.000499755777742 -0.000496963353232 0.000438187450959 0.500109546852 |
Now that you have computed $A^{[2]}$ (in the Python variable “A2“), which contains $a^{2}$ for every example, you can compute the cost function as follows:
$$J = - \frac{1}{m} \sum\limits_{i = 0}^{m} \large{(} \small y^{(i)}\log\left(a^{[2] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[2] (i)}\right) \large{)} \small\tag{13}$$
Exercise: Implement compute_cost() to compute the value of the cost $J$.
Instructions:
- There are many ways to implement the cross-entropy loss. To help you, we give you how we would have implemented
$- \sum\limits_{i=0}^{m} y^{(i)}\log(a^{2})$:12logprobs = np.multiply(np.log(A2),Y)cost = - np.sum(logprobs) # no need to use a for loop!
(you can use either np.multiply() and then np.sum() or directly np.dot()).
|
|
|
|
cost = 0.692919893776
Expected Output:
| cost | 0.692919893776 |
Using the cache computed during forward propagation, you can now implement backward propagation.
Question: Implement the function backward_propagation().
Instructions:
Backpropagation is usually the hardest (most mathematical) part in deep learning. To help you, here again is the slide from the lecture on backpropagation. You’ll want to use the six equations on the right of this slide, since you are building a vectorized implementation.

- Tips:
- To compute dZ1 you’ll need to compute $g^{[1]’}(Z^{[1]})$. Since $g^{[1]}(.)$ is the tanh activation function, if $a = g^{[1]}(z)$ then $g^{[1]’}(z) = 1-a^2$. So you can compute
$g^{[1]’}(Z^{[1]})$ using(1 - np.power(A1, 2)).
- To compute dZ1 you’ll need to compute $g^{[1]’}(Z^{[1]})$. Since $g^{[1]}(.)$ is the tanh activation function, if $a = g^{[1]}(z)$ then $g^{[1]’}(z) = 1-a^2$. So you can compute
|
|
|
|
dW1 = [[ 0.01018708 -0.00708701]
[ 0.00873447 -0.0060768 ]
[-0.00530847 0.00369379]
[-0.02206365 0.01535126]]
db1 = [[-0.00069728]
[-0.00060606]
[ 0.000364 ]
[ 0.00151207]]
dW2 = [[ 0.00363613 0.03153604 0.01162914 -0.01318316]]
db2 = [[ 0.06589489]]
Expected output:
| dW1 | [[ 0.01018708 -0.00708701] [ 0.00873447 -0.0060768 ] [-0.00530847 0.00369379] [-0.02206365 0.01535126]] |
| db1 | [[-0.00069728] [-0.00060606] [ 0.000364 ] [ 0.00151207]] |
| dW2 | [[ 0.00363613 0.03153604 0.01162914 -0.01318316]] |
| db2 | [[ 0.06589489]] |
Question: Implement the update rule. Use gradient descent. You have to use (dW1, db1, dW2, db2) in order to update (W1, b1, W2, b2).
General gradient descent rule: $ \theta = \theta - \alpha \frac{\partial J }{ \partial \theta }$ where $\alpha$ is the learning rate and $\theta$ represents a parameter.
Illustration: The gradient descent algorithm with a good learning rate (converging) and a bad learning rate (diverging). Images courtesy of Adam Harley.


|
|
|
|
W1 = [[-0.00643025 0.01936718]
[-0.02410458 0.03978052]
[-0.01653973 -0.02096177]
[ 0.01046864 -0.05990141]]
b1 = [[ -1.02420756e-06]
[ 1.27373948e-05]
[ 8.32996807e-07]
[ -3.20136836e-06]]
W2 = [[-0.01041081 -0.04463285 0.01758031 0.04747113]]
b2 = [[ 0.00010457]]
Expected Output:
| W1 | [[-0.00643025 0.01936718] [-0.02410458 0.03978052] [-0.01653973 -0.02096177] [ 0.01046864 -0.05990141]] |
| b1 | [[ -1.02420756e-06] [ 1.27373948e-05] [ 8.32996807e-07] [ -3.20136836e-06]] |
| W2 | [[-0.01041081 -0.04463285 0.01758031 0.04747113]] |
| b2 | [[ 0.00010457]] |
4.4 - Integrate parts 4.1, 4.2 and 4.3 in nn_model()
Question: Build your neural network model in nn_model().
Instructions: The neural network model has to use the previous functions in the right order.
|
|
|
|
/opt/conda/lib/python3.5/site-packages/ipykernel/__main__.py:20: RuntimeWarning: divide by zero encountered in log
/home/jovyan/work/Week 3/Planar data classification with one hidden layer/planar_utils.py:34: RuntimeWarning: overflow encountered in exp
s = 1/(1+np.exp(-x))
W1 = [[-4.18494056 5.33220609]
[-7.52989382 1.24306181]
[-4.1929459 5.32632331]
[ 7.52983719 -1.24309422]]
b1 = [[ 2.32926819]
[ 3.79458998]
[ 2.33002577]
[-3.79468846]]
W2 = [[-6033.83672146 -6008.12980822 -6033.10095287 6008.06637269]]
b2 = [[-52.66607724]]
Expected Output:
| W1 | [[-4.18494056 5.33220609] [-7.52989382 1.24306181] [-4.1929459 5.32632331] [ 7.52983719 -1.24309422]] |
| b1 | [[ 2.32926819] [ 3.79458998] [ 2.33002577] [-3.79468846]] |
| W2 | [[-6033.83672146 -6008.12980822 -6033.10095287 6008.06637269]] |
| b2 | [[-52.66607724]] |
4.5 Predictions
Question: Use your model to predict by building predict().
Use forward propagation to predict results.
Reminder: predictions = $y_{prediction} = \mathbb 1 \textfalse = \begin{cases}
1 & \text{if}\ activation > 0.5 \
0 & \text{otherwise}
\end{cases}$
As an example, if you would like to set the entries of a matrix X to 0 and 1 based on a threshold you would do:
|
|
predictions mean = 0.666666666667
Expected Output:
| predictions mean | 0.666666666667 |
It is time to run the model and see how it performs on a planar dataset. Run the following code to test your model with a single hidden layer of $n_h$ hidden units.
|
|
Cost after iteration 0: 0.693048
Cost after iteration 1000: 0.288083
Cost after iteration 2000: 0.254385
Cost after iteration 3000: 0.233864
Cost after iteration 4000: 0.226792
Cost after iteration 5000: 0.222644
Cost after iteration 6000: 0.219731
Cost after iteration 7000: 0.217504
Cost after iteration 8000: 0.219454
Cost after iteration 9000: 0.218607
<matplotlib.text.Text at 0x7f1b55d40b38>
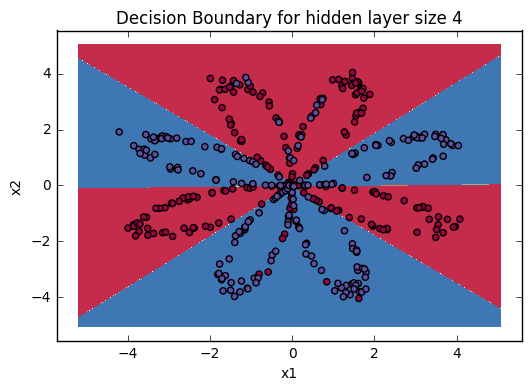
Expected Output:
| Cost after iteration 9000 | 0.218607 |
|
|
Accuracy: 90%
Expected Output:
| Accuracy | 90% |
Accuracy is really high compared to Logistic Regression. The model has learnt the leaf patterns of the flower! Neural networks are able to learn even highly non-linear decision boundaries, unlike logistic regression.
Now, let’s try out several hidden layer sizes.
4.6 - Tuning hidden layer size (optional/ungraded exercise)
Run the following code. It may take 1-2 minutes. You will observe different behaviors of the model for various hidden layer sizes.
|
|
Accuracy for 1 hidden units: 67.5 %
Accuracy for 2 hidden units: 67.25 %
Accuracy for 3 hidden units: 90.75 %
Accuracy for 4 hidden units: 90.5 %
Accuracy for 5 hidden units: 91.25 %
Accuracy for 20 hidden units: 90.0 %
Accuracy for 50 hidden units: 90.25 %

Interpretation:
- The larger models (with more hidden units) are able to fit the training set better, until eventually the largest models overfit the data.
- The best hidden layer size seems to be around n_h = 5. Indeed, a value around here seems to fits the data well without also incurring noticable overfitting.
- You will also learn later about regularization, which lets you use very large models (such as n_h = 50) without much overfitting.
Optional questions:
Note: Remember to submit the assignment but clicking the blue “Submit Assignment” button at the upper-right.
Some optional/ungraded questions that you can explore if you wish:
- What happens when you change the tanh activation for a sigmoid activation or a ReLU activation?
- Play with the learning_rate. What happens?
- What if we change the dataset? (See part 5 below!)
You’ve learnt to:
- Build a complete neural network with a hidden layer
- Make a good use of a non-linear unit
- Implemented forward propagation and backpropagation, and trained a neural network
- See the impact of varying the hidden layer size, including overfitting.
Nice work!
5) Performance on other datasets
If you want, you can rerun the whole notebook (minus the dataset part) for each of the following datasets.
|
|
Congrats on finishing this Programming Assignment!
Reference: